Les trois lois de Képler
Le mouvement des planètes s’étudie dans le repère héliocentrique dont l’origine est le centre d’inertie du Soleil et dont les trois axes sont dirigés vers trois « étoiles fixes ». Il est considéré comme galiléen.
1. Première loi de Képler
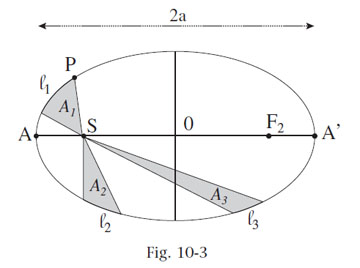
Dans un repère héliocentrique, les centres des planètes décrivent des ellipses dont le centre du Soleil est l’un des foyers. La figure 10-3 vous montre l’ellipse de foyers S (centre du Soleil) et F2 décrite par le centre de la planète P.
2. Deuxième loi de Képler (loi des aires)
Le rayon Planète-Soleil « balaie » des aires proportionnelles aux durées mises pour les « balayer ».
On remarque, figure 10-3, que les aires A1, A2 et A3 sont « balayées » par le rayon PS pendant la même durée : elles sont donc égales. On en déduit, intuitivement, que les arcs parcourus sont tels que : l1 > l2 > l3.
La planète a donc sa plus grande vitesse, sur son orbite, aux alentours du point A qui est le plus proche du Soleil ; au contraire, la vitesse la plus faible est atteinte en A’, point le plus éloigné du Soleil.
Si on assimile l’orbite planétaire à un cercle de centre O, on en déduit que la planète se déplace à vitesse constante : le mouvement est alors considéré comme circulaire uniforme.
3. Troisième loi de Képler
Le carré de la période de révolution est proportionnel au cube du grand axe de l’orbite.
T étant la période (temps nécessaire pour effectuer une révolution sur l’orbite) et 2a = AA’ le grand axe, on écrit :
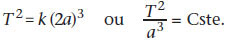
Cette constante k’ est la même pour toutes les planètes du système solaire, ce qui a des applications importantes en astronomie. Pour deux planètes P et P’ du système solaire, on peut écrire :
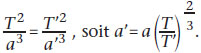
Cela permet de déterminer la valeur de a’ et donc la trajectoire de la planète P’.
Plan du site | Contact | Site réalisé par Mathieu Morainville.
